Smart Materials and Structures: State of the Art and Applications
Ghareeb N and Farhat M
DOI10.21767/2471-9838.100034
Department of Mechanical and Electrical Engineering, Australian College of Kuwait, West Mishref, Kuwait
- *Corresponding Author:
- Ghareeb N
Department of Mechanical and Electrical
Engineering, Australian College of Kuwait
Safat 13015, Kuwait
Tel: +965 1828225
E-mail: n.ghareeb@ack.edu.kw
Received date: August 31, 2018; Accepted date: September 11, 2018; Published date: September 14, 2018
Citation: Ghareeb N, Farhat M (2018) Smart Materials and Structures: State of the Art and Applications. Nano Res Appl. Vol.4 No.2:5. doi:10.21767/2471-9838.100030
Copyright: © 2018 Ghareeb N, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Abstract
The world of materials is an exciting and challenging field of research since it has always played a dominant role in the evolution of human civilization. The demands from aerospace, defence, automotive and industrial branches on more advanced and innovative materials has led to the development of a new generation of materials with much better performance and capabilities than the existing conventional structural and functional materials. As a result, the era of smart materials has started.
Smart materials can change their physical properties in response to a specific stimulus input. However, there is still a blurry image over the types and potential applications of smart materials. The objective of this paper is to define the field of smart materials and structures, together with its current status and potential benefits. However, more focus will be devoted to piezoelectric materials and results are presented and discussed. Finally, and in order to demonstrate the characteristics of one class of smart materials, two numerical examples are proposed and results are presented.
https://betkolikgirisi.com https://betlikeguncel.com https://betparkagiris.com https://bettickett.com https://betturkeyegiris.com https://extrabetgirisi.com https://holiganbeti.com https://ilbete.com https://ikimisligirisi.com https://imajbetegir.com https://jojobeti.com https://kralbetting.com https://mariogiris.com https://marsbahise.com https://meritegiris.com https://milanobeti.com https://piabetegir.com https://redwinegiris.com https://supertotobete.com https://tempobetegir.com
Keywords
Actuators and sensors; Piezoelectric materials; Shape memory alloys; Smart materials
Introduction
"Smart materials” refer to those materials which have the ability to change their composition or structure, their electrical and/or mechanical properties, or even their functions in respond to some environmental stimuli like temperature, pressure, magnetic and electric fields, chemical, or nuclear radiation. Generally, "smart" materials are implanted in systems whose integral properties can be favorably altered in order to respond to the performance needs [1]. The terms "smart" and "intelligent" are used interchangeably for these materials. Takagi defined intelligent materials as those which respond to different environmental changes at the most optimum conditions and manifest their own functions accordingly [2]. Distinguishing Smart and Nano materials, Smart Materials perform both sensing and actuating operations, whereas many Nano materials [3,4] are capable of self-assembly.
The interest of researchers who were engaged in the subject of smart materials have been triggered by the plentiful examples of smart materials that were provided by nature. For example, the leaves of Mimosa pudia collapse suddenly when touched; leaflets of Codariocalyx motorius rotate under exposure to sunlight; sunflowers turn towards the sun; Chameleons change color according to environmental situations [3].
Smart materials are usually utilized as actuators and sensors, and their associated "stimulus" and "response" is depicted in Table 1.
| Variables | Material Class | Stimulus | Response |
|---|---|---|---|
| Sensors | Pyroelectrics | Temperature change | Electric polarization |
| Piezoelectrics | Mechanical strain | Electric polarization | |
| Electrostrictors | Mechanical strain | Electric polarization | |
| Magnetostrictors | Mechanical strain | Change in magnetic field | |
| Electroactive polymers | Mechanical strain | Electric polarization | |
| Electroluminescent | Electric field | Light emission | |
| Photoluminescent | Incident light | Light emission | |
| Electrochromic | Electric field | Color change | |
| Actuators | Piezoelectrics | Electric current | Mechanical strain |
| Electrostrictors | Electric current | Mechanical strain | |
| Magnetostrictors | Magnetic field | Mechanical strain | |
| Shape memory alloys | Temperature change | Mechanical strain | |
| Electroactive polymers | Electric field | Mechanical strain | |
| Electrorheological fluids | Electric field | Viscosity change | |
| Magnetorheological fluids | Magnetic field | Viscosity change |
Table 1: Sensor and actuator material classes.
Literature Review
Major advantages of smart material actuators and sensors include high energy density, fast response, compact size, and fewer moving parts. Some disadvantages include limited strain outputs, limited blocking forces, high cost, and sensitivity to harsh environmental conditions [4,5]. The nonlinear properties of these materials present one of the major hurdles for their application. They are more likely to be observed as hysteresis. This nonlinear behavior is described [6,7] among others. Recent progress in smart materials for distributed actuators and sensors has triggered a considerable interest in smart structures. Once smart materials are bonded to or embedded in conventional structures, those structures obtain sensing, actuating and processing or controlling capabilities, which are the basic active features of smart or intelligent structures [8]. A smart structure can thus sense external disturbances and respond to those with active control in real time to meet the desired requirements [9]. This means, it has the ability to sense a variable such as temperature, pressure, strain; diagnose the nature and extent of any problem; initiate an appropriate action to address the identified problem; and finally to store the processes in memory and "learn" to use the actions taken as a basis next time around [10]. Smart structures can be classified based on the level of sophistication, and the relationship between these structure types is depicted in Figure 1.
A sensory structure thus contains sensors but no actuators for monitoring the state of the structure. An adaptive structure has no sensors but possesses actuators that enable the alteration of system states in a controlled manner. A controlled structure results from the combination of a sensory and an adaptive structure in which both sensors and actuators are integrated in a closedloop system for the purpose of actively controlling the system states. An active structure is a controlled structure that contains integrated sensors and actuators which fulfill both structural and control functions. An intelligent structure is an active structure that has highly integrated control logic and electronics in addition to distributed actuators and sensors [11,12].
Smart structures are used in several shape and vibration control applications. Micro positioning, satellite antenna shape control, space structure shape correction, and automatic flow control valves are some of the practical examples of shape control applications. Vibration control applications include active suspension systems for vehicles and active vibration control in aircraft such as the control of aeroelastic instabilities like flutter, divergence, and aircraft vibration [13,14].
Smart materials can be subdivided into materials that exhibit either a direct or an indirect coupling. Piezoelectric materials, shape memory alloys, magneto-strictive ceramics and magnetic shape memory alloys are examples of active materials that exhibit a direct coupling. This means that either the mechanical or the non-mechanical field can serve as an input while the other as the output. In contrast, for active materials such as electrorheological fluids (ERF) and magneto-rheological fluids (MRF), a change in the electric field or the magnetic field can indirectly couple with the mechanical behavior through a change in the viscosity of the fluid.
This remaining part of this paper outlines the development and state of the art of piezoelectric materials. In addition, a numerical example which demonstrates the characteristics of piezoelectric materials is proposed.
Piezoelectric materials
Piezoelectricity could be referred to as the capability of some materials, particularly in the form of crystals and ceramics, to produce an electric potential as a response to an input in the form of an applied mechanical stress [15]. This phenomenon is defined as the “direct piezoelectric effect”. The converse (or reverse) piezoelectric effect is, however, when the materials produce a stress and/or strain (output) when an electric field is applied (input). In 1880, Pierre and Jacques Curie published the first experimental demonstration of a connection between macroscopic piezoelectric phenomena and crystallographic structure. In this experiment, a mechanical stress was applied on a specially prepared crystals and a conclusive measurement of surface charges was performed. These specially prepared crystals were mainly composed of quartz, Rochelle salt, tourmaline, cane sugar and topaz.
Discussion
During World War I, the French Langevin and his co-workers invented an ultrasonic submarine detector which was the first real application work on a piezoelectric device [16]. This detector comprised a mixture of thin quartz crystals bonded between two steel plates and mounted in a housing which was adequate for submersion. The resonant frequency of that composite was about 50 Hz. With this instrument, the objective of emitting a high frequency “chirrup” underwater and timing the return echo to measure the depth was achieved.
Following World War I, the majority of the classic piezoelectric applications was perceived and brought to practice. These applications included accelerometers, signal filters, microphones, ultrasonic transducers, etc.
It must be mentioned here that available materials at that time had only a limited device performance and thus a restricted commercial exploitation.
During World War II, it was revealed that certain ceramic materials (called ferroelectrics) exhibit a much higher dielectric constants than common quartz crystals (up to 100 times more) with improved other piezoelectric properties and astonishing performance. These piezoelectric ceramics, which could be manufactured easily, provoked an intense development and research into piezoelectric devices. All this has contributed to establishing an entirely new method of piezoelectric device development, where a material is tailored to perform a specific application [17].
After World War II, the materials and device development was basically dominated by industrial companies in the U.S. and a huge number of applications was performed. This included among others piezo ignition systems, powerful sonars, sensitive microphones, small audio tone transducers, snap action relays, ceramic phono cartridges, etc. It must be mentioned here that the majority of materials in common use today were developed by 1970, however their commercial application was not revealed at that time due to confidentiality in the U.S.
In contrast to the Americans, manufacturers from other countries like Japan didn’t strive getting patents and thus constraining their inventions since they were aiming at creating new markets to sell their products. These products included audio transducers for direct connection with electric circuits, piezoelectric igniters for gas-grill lighters and small engine ignition systems, piezoelectric filters for radios and TVs, television remote controls composed of ultrasonic transducers that are capable of transmitting sound waves through air, etc.
The search on piezoelectric product opportunities is currently still in progress and the opportunity for future important technical developments appears to be assured.
Numerical examples of smart structures
In this section, two examples will be presented to demonstrate the converse (or reverse) piezoelectric effect and the direct piezoelectric effects. These are explained in more details in the author’s Ph.D. thesis [18]. In the first example, numerical results are compared to experimental ones, and in the second example they are compared to results from literature.
Example 1: Cantilevered piezoelectric beam with double PZT patches: The objective of the first numerical example is to predict the converse piezoelectric effect of a piezoelectric beam, and to verify that the natural frequency of this structure in open-circuit (OC) state is smaller than the natural frequency in short-circuit (SC) state, as proven in some references like [19,20].
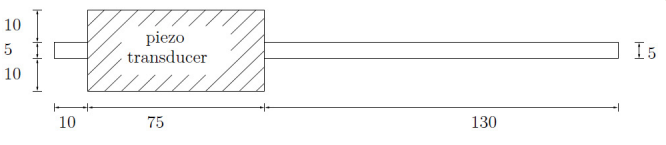
The steel beam is idealized as a single layered beam structure. An adhesive layer is used between the PZT patches and the steel beam as shown in Figure 2. The geometrical dimensions are depicted in Figure 3, and the thickness and material properties are shown in Table 2. The piezoelectric patches are polarized in the through-thickness direction and the properties of the piezoelectric material used are shown in Table 3. The beam longitudinal direction designates the local x-direction, and the beam cross-section represents the local y- and z-directions. The beam is clamped at its left end and it has elastic and isotropic material. The finite element analysis (FEA) software ABAQUS is used in this example. A perfect bond is defined between bonding layer and the steel beam, as well as between the bonding layer and each piezoelectric patch. As a boundary condition, a zero potential is assigned to the piezo surfaces throughout the analysis, and the Piezoelectric material PIC 151 was used.
| Property | Steel | Piezo (PIC 151) | Epoxy |
|---|---|---|---|
| Thickness (mm) | 0.5 | 0.25 | 0.036 |
| Young’s modulus (GPa) | 210 | 66.667 | 3.5464 |
| Poisson’s ratio (-) | 0.3 | 0.3 | 0.4 |
| Density (kg/m3) | 7900 | 7800 | 1180 |
Table 2: Material properties of the structure components.
| Parameters | PIC 151 |
|---|---|
| Permittivity in polarization direction (10-8 [F/m]) | 2.124 |
| Permittivity perpendicular to polarization direction (10-8 [F/m]) | 1.75 |
| Piezoelectric constant d31 (10-12 [C/N]) | -210 |
| Piezoelectric constant d33 (10-12 [C/N]) | 500 |
Table 3: Piezoelectric properties of the piezo material.
In this example three analysis steps are done:
1. An electric potential of 1000 V is applied and the induced deformation is measured.
2. The applied potential is reduced to 0 V and then a SC modal analysis is carried out.
3. The OC conditions are now applied and then an OC modal analysis is performed.
The deformed shape of the transducer from Step 1 is shown in Figure 4. The first two natural frequencies of the modal analysis in Steps 1 and 2 are depicted in Table 4. The results are similar to those from experiment. The idea behind the modal analysis was, again, to prove that the frequency of the piezoelectric beam under OC conditions is greater than that under the SC conditions.
| Natural frequency number | Natural frequency type | SC | OC |
|---|---|---|---|
| First | Simulation | 10.11 | 10.73 |
| Experiment | 9.64 | 9.78 | |
| Second | Simulation | 34.60 | 34.75 |
| Experiment | 34.16 | 34.24 |
Table 4: The natural frequencies of the smart beam (rad/s).
Example 2: Cantilevered Piezo-laminated Beam with PZT Sensor Patch: The second numerical example illustrates the direct piezoelectric effect. A cantilevered beam consisting of an isotropic structure with a PZT sensor patch attached perfectly at a distance of 60 mm of the clamping constraint is considered. The geometry is shown in Figure 5.
The same model is found in references like [21,22]. In the first reference, the third-order shell deformation theory (TOSD) was used and the second reference used the first-order shear deformation theory (FOSD). A step force of 0.6 N is applied at the tip of the beam. The material parameters of the beam are depicted in Table 5. The FE software ABAQUS is also used in this example. The graph of the sensor output voltage over time is shown in Figure 6. The "Actual" results are those predicted by the FE software and they are compared to results available [21], and results show good agreement. The tip displacement at the beam tip is displayed in Figure 7, and the values are similar to those from literature too [23,24].
| Parameters | Beam (G1195) | PZT (T300/976) |
|---|---|---|
| Young’s modulusÃÆââ¬Å¡Ãâà(GPa) | 197 | 67 |
| Poisson’s ratio (-) | 0.33 | 0.33 |
| Density (kg/m3) | 7900 | 7800 |
| d31 (m/V) | - | 1.712 e-10 |
| ÃÆââ¬Å¡ÃâàPermittivity (F/m) | - | 2.03e-8 |
Table 5: Patient post-operative LOS and correlation with patient age.
Conclusion
In this paper, a state of the art of smart materials was presented including history and applications. A special focus was put on piezoelectric materials and their industrial applications. Finally, two numerical examples were proposed to demonstrate the properties of piezoelectric materials and results were compared to those from experiment and from literature.
References
- Reece P (2006) Smart materials and structures. Nova Science Publishers, New York, USA.
- Takagi T (1990) A concept of intelligent materials. J Intell Material Syst Struct 1: 149-156.
- Hussein AK, Li D, Kolsi L, Kata S, Sahoo B (2017) A review of nano fluid role to improve the performance of the heat pipe solar collectors. Energy Procedia 109: 417-424
- Serrano E, Rus G, Garcia Martinez J (2009) Nanotechnology for sustainable energy. J Renew Sustain Energy 13: 2373-2384
- Hu J, Meng H, Li G, Ibekwe SI (2012) A review of stimuli-responsive polymers for smart textile applications. Smart Mater Struct 5: 1-23.
- Lane R, Craig B (2003) Materials that sense and respond: An introduction to smart materials. AMPTIAC 2: 9-14.
- Sarawate N (2008) Characterization and modeling of the ferromagnetic shape memory alloy for sensing and actuation. PhD thesis, Ohio State University. USA.
- Fan B (2010) Non-linearity modeling of smart materials and structures. PhD thesis, University of Houston.
- Yao L et al. (2004) Nonlinear static characteristics of piezoelectric bending actuators under strong applied electric field. Sens Actuators 115: 168-175.
- Nguyen V (2005) Piezoelectric actuator design optimization for shape control of smart composite plate structures. PhD thesis, The University of Sydney, Sydney, Australia.
- Uelker F (2003) Active vibration control of smart structures. MasterÃÆâÃâââ¬Ãâââ¢s thesis, The Middle East Technical University, Turkey.
- Srinivasan A and McFarland D (2001) Smart structures, analysis and design. Cambridge University Press, USA.
- Huang D (1999) Approximate analytical solutions for vibration control of smart composite beams. MasterÃÆâÃâââ¬Ãâââ¢s thesis, Peninsula Technikon, Cape Town, South Africa.
- Sunar M, Rao S (1999) Recent advances in sensing and control of flexible structures via piezoelectric materials technology. American Society of Mechanical Engineers 1: 1-16.
- Kandagal S, Venkatraman K (2006) Piezo-actuated vibration and flutter control. Def Sci J 4: 615-626.
- Periasamy R (2008) Shape control of composite structures with optimally placed piezoelectric patches. MasterÃÆâÃâââ¬Ãâââ¢s thesis, University of Waterloo, Canada.
- Skoog D, Holler FJ, Crouch SR (2007) Principles of instrumental analysis. Cengage Learning.
- Graff K (1981) History of ultrasonics. Phys Acoustics 15: 1-97.
- APC International Limited (2011) Piezoelectric ceramics: Principles and applications.
- Ghareeb N (2013) Design and implementation of linear controllers for the active control of reduced models of thin-walled structures. PhD thesis, The RWTH Aachen University of Technology, Germany.
- Jalili N (2010) Piezoelectric-based vibration control. Springer, UK.
- Locatelli G (2001) Piezo-actuated adaptive structures for vibration damping and shape control, modeling and testing. PhD thesis, Technical University of Munich, Germany.
- Vu TD (2011) Geometrically nonlinear higher-order shear deformation FE analysis of thin-walled smart structures. PhD thesis, The RWTH Aachen University of Technology, Germany.
- Lentzen S, Schmidt R (2005) A geometrically nonlinear finite element for transient analysis of piezo-laminated shells. Proceedings of the fifth EUROMECH nonlinear dynamics conference 1: 2429-2500.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences